Probabilidad

     Las probabilidades constituyen una rama de las matemáticas que se ocupa de medir o determinar cuantitativamente la posibilidad de que un suceso o experimento produzca un determinado resultado. La probabilidad está basada en el estudio de la combinatoria y es fundamento necesario de la estadística.

     La probabilidad matemática se utiliza mucho en las ciencias físicas, biológicas y sociales, así como en el comercio y la industria. Se aplica a muchas áreas tan dispares como la genética, la mecánica cuántica y los seguros. También estudia problemas matemáticos teóricos de gran importancia y dificultad y está bastante relacionada con la teoría del análisis matemático, que se desarrolló a partir del cálculo.

     La probabilidad mide la mayor o menor posibilidad de que se dé un determinado resultado (suceso o evento) cuando se realiza un experimento aleatorio.

Para calcular la probabilidad de un evento se toma en cuenta todos los casos posibles de ocurrencia del mismo; es decir, de cuántas formas puede ocurrir determinada situación.

     Los casos favorables de ocurrencia de un evento serán los que cumplan con la condición que estamos buscando.

La probabilidad toma valores entre 0 y 1 (o expresados en tanto por ciento, entre 0% y 100%):

El valor cero corresponde al suceso imposible; ejemplo: lanzamos un dado al aire y la probabilidad de que salga el número 7 es cero.

El valor uno corresponde al suceso seguro, ejemplo: lanzamos un dado al aire y la probabilidad de que salga cualquier número del 1 al 6 es igual a uno (100%).

El resto de sucesos tendrá probabilidades entre cero y uno: que será tanto mayor cuanto más probable sea que dicho suceso tenga lugar.

Métodos de medición de Probabilidad:

     Uno de los métodos más utilizados es aplicando la Regla de Laplace: define la probabilidad de un suceso como el cociente entre casos favorables y casos posibles.

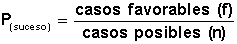
Ejemplos:

a) Probabilidad de que al lanzar un dado salga el número 2:

El caso favorable (f) es tan sólo uno (que salga el dos), mientras que los casos posibles (n) son seis (puede salir cualquier número del uno al seis).

Por lo tanto:

 (o lo que es lo mismo, 16,6%)

Por lo tanto:b) Probabilidad de que al lanzar un dado salga un número par: en este caso los casos favorables (f) son tres (que salga el dos, el cuatro o el seis), mientras que los casos posibles (n) siguen siendo seis.

  (o lo que es lo mismo, 50%)

c) Probabilidad de que al lanzar un dado salga un número menor que 5: en este caso tenemos cuatro casos favorables (f) (que salga el uno, el dos, el tres o el cuatro), frente a los seis casos posibles.

Por lo tanto:
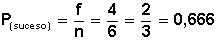 (o lo que es lo mismo, 66,6%)

d) Probabilidad de ganarse el premio mayor de una lotería en la que juegan 100.000 númerosnos: tan sólo un caso favorable (f), el número que jugamos, frente a los 100.000 casos posibles (n).

Por lo tanto:

 (o lo que es lo mismo, 0,001%)

Condiciones importantes:

Para poder aplicar la Regla de Laplace el experimento aleatorio tiene que cumplir dos requisitos:

a) El número de resultados posibles (sucesos eventos) tiene que ser finito. Si hubiera infinitos resultados, al aplicar la regla "casos favorables dividido por casos posibles" el cociente siempre sería cero.

b) Todos los sucesos o eventos tienen que tener la misma probabilidad. Si al lanzar un dado, algunas caras tuvieran mayor probabilidad de salir que otras, no podríamos aplicar esta regla.

     A la regla de Laplace también se le denomina "probabilidad a priori", ya que para aplicarla hay que conocer antes de realizar el experimento cuales son los posibles resultados y saber que todos tienen las mismas probabilidades.

     Cuando se realiza un experimento aleatorio un número muy elevado de veces, las probabilidades de los diversos posibles sucesos empiezan a converger hacia valores determinados, que son sus respectivas probabilidades.

Ejemplo:

     si lanzo una vez una moneda al aire y sale "cara", quiere decir que el suceso "cara" ha aparecido el 100% de las veces y el suceso "cruz" el 0%.

Si lanzo diez veces la moneda al aire, es posible que el suceso "cara" salga 7 veces y el suceso "cruz" las 3 restantes. En este caso, la probabilidad del suceso "cara" ya no sería del 100%, sino que se habría reducido al 70%.

     Si repito este experimento un número elevado de veces, lo normal es que las probabilidades de los sucesos "cara" y "cruz" se vayan aproximando al 50% cada una. Este 50% será la probabilidad de estos sucesos según el modelo frecuentativo.